Poisson Process

왜 Poisson Process를 공부하는가?

Linkedin에서 현업 데이터 분석가 분들의 인사이트를 읽다보면,

'얼마나 많이'보다 '언제 일어나는가'에 대한 문제를 더 자주 고민하시는 것을 많이 접할 수 있었다.

 

예를 들어,

• "한 시간 뒤 고객 몇 명이 우리 웹사이트에 들어올까?"
• "광고를 본 뒤 유저가 앱을 다시 켜는 데까지 시간이 얼마나 걸릴까?"

와 같은 시간 기반의 사건들의 확률을 이해하기 위해선 다루는 도구에 대한 이해도 필요하다.

Poisson Process는 이런 시간 기반의 사건들을 수학적으로 풀 수 있는 도구 중 하나이다.

 

 

평균만 본다고 예측이 되는 게 아니다

 

💬 우리 콜센터는 시간당 평균 12콜이 와요

 

→ 이 말로는 10분동안 5콜이 몰릴 수도, 0콜이 올 수도 있다는 걸 설명할 수 없다.

 

 

그래서 등장하는 게 Poisson Process이다.

 

"이벤트가 시간에 따라 얼마나 자주 발생하는지"를 수학적으로 모델링하는 것으로,

단순 카운트가 아니라, 시간이라는 축 위에서 사건의 확률을 추론할 수 있게 해준다.

 

 

 

---

Poisson Distribution의 정의

Poisson Distribution은 단순히 "사건이 얼마나 자주 일어나는가"를 설명하는 분포가 아니라,

시간(t)이라는 연속적 흐름 속에서 불연속적인 사건이 '몇 번' 발생하는지를 모델링하는 것이다.

 

→ 이 MGF는 Poisson 분포를 완전히 특징짓는 지표로, 정규성을 다룰 때에도 중요하다.

Poisson Process의 조건

 

✅ 목표:

Poisson Process의 목표는

{N(t) : t≥0} 에서 시각 t 동안 발생한 사건 수 N(t)가 Poisson Distribution(λt)을 따른다는 것을 보이는 것

 

 

Poisson Distribution Property

 

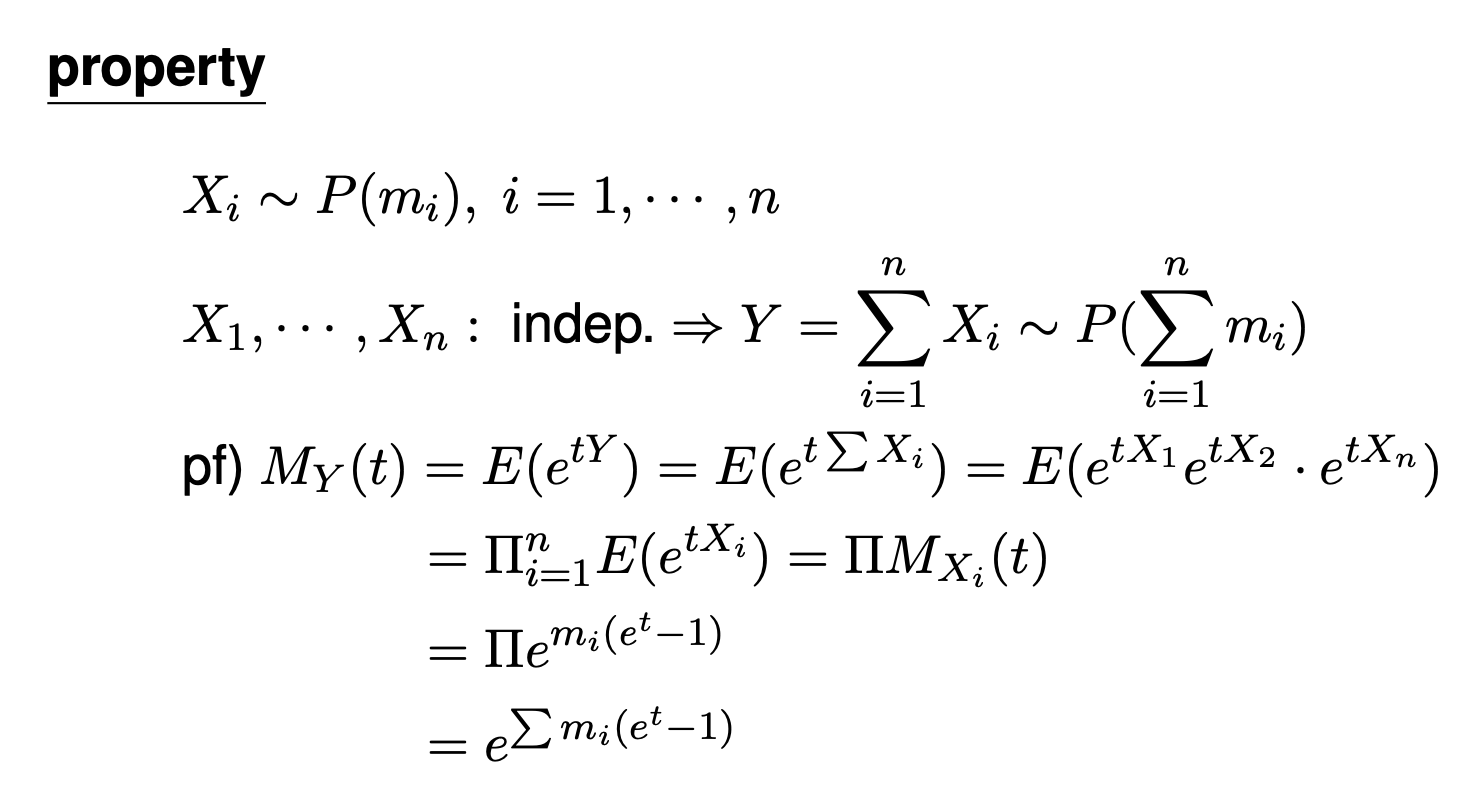
서로 독립인 X1, ..., Xn 사건 수의 합은 사건 간 간격이 i.i.d ~ Exponential(λ)로,

이로부터 도착 시간이 증가하면서 누적 사건 수 N(t)가 Poisson 분포를 따른다는 의미이다.

 

Poisson Process는 기억을 못 해요 (Memoryless Property)

"지금까지 아무 일도 안 일어났다는 사실이, 다음에 일어날 확률을 바꾸지 않는다"

→ 이게 바로 Memoryless Property(무기억성)이며, 본질적으로는 Exponential 분포의 성질에서 유도된다.

 

P(T > s + t | T > s) = P(T > t)

 

복잡해 보이지만, 이미 s만큼 기다렸다고 해도, 앞으로 더 기다릴 시간은 '처음부터 기다리는 것과 같다.'는 의미이다.