Moment Generating Function

모멘트(moment)

확률변수의 "모양(형태)"을 숫자로  요약한 값

 

확률변수의 분포가 어디쯤에 몰려 있는지, 얼마나 퍼져 있는지, asymmetric한지, 뾰족한지 같은 걸 수치화한 것 -> 모멘트

모멘트 종류	정의	의미
1차 모멘트	E[X]	평균 (중심 위치)
2차 중심 모멘트	E[(X−μ)^2]	분산 (퍼짐 정도)
3차 중심 모멘트	E[(X-μ)^3]	왜도 (비대칭성)
4차 중심 모멘트	E[(X−μ)^4]	첨도 (뾰족함)

※ 중심 모멘트에서 μ=E[X]는 평균

 

 

---

왜 중요한가?

👉 확률분포의 모양을 숫자로 설명해줘서
👉 우리가 데이터를 요약하고 비교하고 추론하는 데 꼭 필요하기 때문

 

즉, 분포의 특성을 알아야 데이터를 이해하고 모델링할 수 있고,

모멘트는 분포의 모양을 한 줄 요약해주는 것이다.

 

 

MGF(Moment Generating Function)란 이 모멘트들을 한 번에 뽑아낼 수 있게 해주는 유용한 함수

 

 

 

왜 MGF를 쓰는가?

확률분포를 요약하는 대표적인 수치는?

평균(1차 moment), 분산(2차 moment)와 같은 모멘트

 

이러한 모멘트들을 따로따로 계산하는 것이 아닌, 한 번에 계산하고, 나아가 분포 자체를 알아낼 수 있다면 편하지 않을까?

👉 그걸 가능하게 해주는 게 Moment Generating Function(MGF)

 

 

 

---

MGF의 정의

 

 

 

그런데 말이 너무 어렵다.

하나씩 풀어보자.

 

e^(tX)의 기대값이 존재한다?

어떤 확률변수 X에 대해 E(e^(tX))라는 값을 계산할 수 있다는 말이다.

여기서 E[•]는 평균 또는 기대값을 의미한다.

즉, 확률변수 X를 가지고 지수함수 e^(tX)를 만든 다음, 그 함수의 평균값을 구한다는 뜻

 

E(e^(tX))가 존재하려면 너무 발산하지 않고 적분이 수렴해야 하므로, t는 너무 큰 값이 되면 안될 것이다.
그래서 -h < t < t 라는 조건이 붙은 것.

 

 

 

---

왜 "Moment Generating"이냐?

우선, Talyor Series를 먼저 이해해야 한다.

테일러 전개의 Motive는 다음과 같다.

 

복잡한 함수식($e^x$, $logx$, $\sinx$)와 같은 함수가 존재할 때,

딱 떨어지는 해석적 계산이 어렵고 확률분포나 기대값을 구할 때 너무 복잡해지는 문제가 있다.

 

복잡한 함수를 간단한 다항식으로 바꿔 근사해서 해결하자는 말.

복잡한 함수 값 ≈ 함수의 도함수들을 이용한 다항식  ⇒ Taylor Series

테일러 전개의 복습

 

 

즉, $E[e^{tX}]$을 다항식으로 전개해서 모멘트를 얻는 것 = MGF 자체가 테일러 전개 기반

$= 1 + \mu t + \frac{E[X^2]}{2!}t^2 + \cdots$

 

그래서 이름이 "MGF = Moment Generating Function"인 것이다.

모멘트를 만들어주는 함수이므로!

 

---

예제: X가 Uniform Distribution일 때 Mgf 구하기

X~U(0,1)라고 하자.

즉, 

 

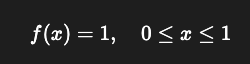
이때 X의 Mgf M(t)를 구하시오.

 

 

 

---

모델링에서도 중요한 이유

머신러닝에서는 데이터 전처리할 때
→ 왜도 높으면 log 변환
→ 분산 크면 Standardization
→ 평균 중심 맞춤

 

즉, 통계모형에서 MGF를 사용해 분포를 식별하거나
모멘트를 통해 추정량의 성질 분석이 가능하니 꼭 알아둬야 할 개념이다.