2025. 3. 14. 22:00ㆍData Analysis/Computer Science
자료구조가 중요한 이유

코딩을 처음 시작했을 때를 생각해보면,
단순히 내가 작성한 코드가 올바르게 작동하는 지가 가장 중요했다. (지금도 별반 다르지 않다.)
하지만 동아리에서 흔히 코딩좀 치는(?) 형들이 서로 코드 리뷰하는 대화를 들어보면,
그렇게 잘 짠 코드는 아닌듯?
하는 대화를 들을 때가 많다.
그렇다면 '잘 짠 코드' 란 뭘까?
고품질 코드
'잘 짠 코드', 즉 고품질 코드는 바로 다음을 만족하는 코드이다.
1. 코드의 유지보수성 (Maintainability)
👉 코드가 직관적이며 쉽게 수정, 확장될 수 있는가?
2. 코드의 효율성 (Efficiency)
👉 코드가 빠르고 적은 리소스를 사용하도록 최적화되었는가?
위 두 가지를 만족하는 것이 뛰어난 개발자의 역량이며,
이를 위해 적절한 자료구조 와 알고리즘 선택이 필수적이다.
자료구조
자료구조는 같은 데이터를 다양한 방식으로 조직(Organizing)하는 방법론이다.
하지만 단순한 데이터 저장 방식이 아니라,
데이터 구조가 프로그램 성능에 미치는 영향을 고려하는 것이 중요하다.
🚨 적절한 자료구조 선택은 프로그램의 성능을 결정짓는 핵심 요소임을 기억하자.
자료구조의 기본 연산
자료구조의 성능을 이해하려면, 코드가 자료구조와 어떻게 상호작용하는지를 분석해야 한다.
대부분의 자료구조는 아래 네 가지 기본 연산을 수행한다.
읽기(Read) : 특정 위치에 저장된 데이터를 가져온다.
검색(Search) : 원하는 데이터를 찾아 해당 위치(Index)를 반환한다.
삽입(Insert) : 새로운 데이터를 자료구조에 추가한다.
삭제(Delete) : 특정 데이터를 제거한다.
각 연산의 속도는 자료구조에 따라 크게 차이가 나며,
이를 정량적으로 측정하는 것이 중요하다.
알고리즘 성능 측정: 시간 복잡도(Time Complexity)

연산의 속도를 측정할 때는 단순히 실제 실행 시간을 기준으로 하지 않는다.
왜 실행 시간이 기준이 아니지 ?
그 이유는 크게 두 가지이다.
1. 하드웨어(컴퓨터 성능)에 따라 실행 시간이 달라진다.
2. 같은 코드라도 실행 환경(운영체제, 메모리 상황)에 따라 다르게 동작할 수 있다.
따라서 연산 속도를 비교할 때는 "얼마나 많은 단계(Step)가 필요한가?" 를 기준으로 측정해야 한다.

다음은 초등학생도 이해할 수 있는 알고리즘 성능 평가 문제이다.
- 알고리즘 A: 데이터 검색에 5단계가 필요
- 알고리즘 B: 데이터 검색에 500단계가 필요
👨🏻🏫 어떤 알고리즘의 성능이 더 빠를까?
🙋🏻♂️ 에이~
그렇다. 모든 환경(하드웨어)에서 A가 B보다 빠를 가능성이 높다.
이처럼 단계 수를 기준으로 성능을 분석하는 것이 시간 복잡도 분석의 핵심이다.
그러나, 입력 크기(n)가 매우 커진다면?
점근적 표기법(Asymptotic Notation)
점근적 표기법을 사용하면, 입력 크기 n이 증가할 때
알고리즘의 성능이 어떤 속도로 증가하거나 감소하는지를 분석할 수 있다.

즉, 점근적 표기법은 알고리즘이 실행되는 Worst, Best, Average 시간 복잡도를 나타내는 방법이다.
점근적 표기법의 종류
접근적 표기법은 대표적으로 O(빅오), Ω(오메가), Θ(세타) 로 구분된다.
각각의 의미와 수식은 다음과 같다.
✔️ 최악의 경우 (Worst-case) 에 대한 성능을 나타냄
✔️ 알고리즘이 가장 느리게 동작하는 시간 복잡도
✔️ 상한(Bound on the worst case) 을 의미
빅오 표기법(Big-O)
✅ 알고리즘이 최악(Worst-case) 상황에서 보장하는 성능
✅ 가장 많이 사용되는 표기법
✅ 시간 복잡도의 상한(Upper Bound) 을 의미
가장 많이 사용되며, 최악의 경우 알고리즘의 수행 시간이 어떻게 증가하는지를 나타낸다.
즉, 시간 복잡도의 Bounded Above를 의미하며, f(n)의 성장이 어느 정도 이하임을 보장한다.
예를 들어,
- 선형 탐색(Linear Search): O(n) 👉 최악의 경우 끝까지 탐색
- 이진 탐색(Binary Search): O(logn) 👉 최악의 경우 로그 단위로 감소
- 버블 정렬(Bubble Sort): O(n^2) 👉 모든 원소를 비교
이를 수식으로 표현하면,
한 함수 가 O(g(n)) 에 속한다는 것은,
적당한 상수 c 와 n0 가 존재하여 다음이 성립함을 의미한다.

오메가 표기법 (Big-Ω)
✅ 알고리즘이 최상의 경우(Best-case) 에 보장하는 성능
✅ 시간 복잡도의 하한(Lower Bound) 을 의미
예를 들어,
- 정렬된 배열에서의 선형 탐색: Ω(1) 👉 첫 번째 원소가 찾고자 하는 값이면 한 번만 탐색
- 선택 정렬(Selection Sort): Ω(n²) 👉 항상 모든 원소를 비교해야 하므로 최상의 경우도 O(n²)
이를 수식으로 표현하면,
한 함수 가 Ω(g(n)) 에 속한다는 것은,
적당한 상수 c 와 n0 가 존재하여 다음이 성립함을 의미한다.
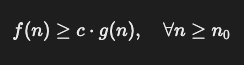
세타 표기법 (Big-Θ)
✅ 알고리즘이 평균적으로 보장하는 성능
✅ 상한과 하한이 동일할 때 사용 (Upper & Lower Bound)
✅ 가장 정확한 시간 복잡도 표현
예를 들어,
- 버블 정렬(Bubble Sort): Θ(n²) 👉 최악, 최상, 평균 모두 O(n²)
- 퀵 정렬(Quick Sort): Θ(n log n) 👉 최악은 O(n²) 이지만 평균적으로 n log n
이를 수식으로 표현하면,
한 함수 가 Ω(g(n)) 에 속한다는 것은,
적당한 상수 c1, c2 와 n0 가 존재하여 다음이 성립함을 의미한다.

즉, 시간 복잡도를 올바르게 이해하고 사용하면,
알고리즘의 성능을 더욱 효과적으로 비교하고 최적화할 수 있다.
알고리즘의 역할
올바른 자료구조만 선택하면 코드 성능 효율성 문제는 해결될까?
위에서도 말했듯이 모든 문제는 Step by Step이다.
즉, 사용할 알고리즘을 적절하게 선택하는 문제 역시 중요하다.

자료구조가 데이터를 저장하고 관리하는 방식이라면, 알고리즘은 특정 문제를 해결하기 위한 절차이다.
같은 문제를 해결하더라도, 어떤 어떤 알고리즘을 사용하느냐에 따라 실행 속도가 크게 달라질 수 있으며,
알고리즘 선택은 프로그램의 실행 시간, 메모리 사용량, 확장성에 영향을 미친다.
결론
✅ 적절한 자료구조 선택이 프로그램의 성능을 결정한다.
✅ 효율적인 알고리즘 선택이 실행 속도를 크게 향상시킨다.
✅ 시간 복잡도를 고려하여 O(1) > O(log n) > O(n) > O(n log n) > O(n²) > O(2ⁿ) > O(n!) 순으로 성능을 분석해야 한다.
'Data Analysis > Computer Science' 카테고리의 다른 글
| CPU와 기억장치, 메모리 (3) | 2025.08.04 |
|---|---|
| 운영체제와 컴퓨터 (4) | 2025.08.01 |
| 추상 자료형 (Abstract Data Type) (0) | 2024.07.04 |
| Network Layer : Data Plane (1) | 2024.06.15 |
| Transport Layer - TCP Congestion Control (0) | 2024.06.15 |